Prueba t de Student: una guía práctica para el análisis de datos
En el ámbito de la estadística, la prueba t de Student es una herramienta fundamental para comparar dos grupos de datos y determinar si existe una diferencia significativa entre sus medias. Esta prueba se utiliza ampliamente en campos como la investigación médica, la ingeniería y la economía, entre otros. En este artículo, exploraremos en profundidad la prueba t de Student, su aplicación práctica y las diferentes variantes que existen.
¿Qué es la prueba t de Student?
La prueba t de Student es una prueba estadística paramétrica que se utiliza para comparar las medias de dos grupos de datos. La prueba asume que los datos se distribuyen normalmente y que las varianzas de los grupos son iguales. Esta prueba lleva el nombre de William Sealy Gosset, quien la desarrolló mientras trabajaba en la cervecería Guinness en Dublín y publicó sus hallazgos bajo el seudónimo de "Student".
La prueba t de Student se basa en la distribución t de Student, una distribución de probabilidad que se utiliza para estimar la media de una población cuando el tamaño de la muestra es pequeño. La distribución t es similar a la distribución normal, pero presenta colas más gruesas, lo que la hace más adecuada para datos con una menor cantidad de observaciones.
Tipos de pruebas t de Student
Existen dos tipos principales de pruebas t de Student:
Prueba t de muestra única
Se utiliza para comparar la media de una muestra con un valor conocido de la población. Por ejemplo, si queremos determinar si la altura promedio de los estudiantes de una universidad es diferente de la altura promedio de la población general, podríamos utilizar una prueba t de muestra única. Esta prueba se utiliza cuando se quiere comparar un grupo de datos con un valor teórico o con la media de la población. Se utiliza para determinar si la media de la muestra es significativamente diferente de un valor específico.
Prueba t de muestras independientes
Se utiliza para comparar las medias de dos grupos independientes de datos. Por ejemplo, si queremos determinar si existe una diferencia significativa en la efectividad de dos tratamientos diferentes para una enfermedad, podríamos utilizar una prueba t de muestras independientes. Esta prueba se utiliza para determinar si las medias de dos grupos independientes de datos son significativamente diferentes. Se utiliza para comparar dos grupos que no están relacionados entre sí.
Prueba t de muestras pareadas
Se utiliza para comparar las medias de dos grupos relacionados de datos. Por ejemplo, si queremos determinar si existe un cambio significativo en la presión arterial de un grupo de pacientes después de tomar un nuevo medicamento, podríamos utilizar una prueba t de muestras pareadas. Esta prueba se utiliza para comparar dos grupos que están relacionados entre sí, como antes y después de una intervención.
Cómo se realiza la prueba t de Student
Para realizar una prueba t de Student, se necesitan los siguientes pasos:
- Definir la hipótesis nula y la hipótesis alternativa: La hipótesis nula establece que no hay diferencia entre las medias de los grupos. La hipótesis alternativa establece que sí hay una diferencia.
- Calcular el estadístico t: El estadístico t es una medida de la diferencia entre las medias de los grupos, en relación con la variabilidad de los datos.
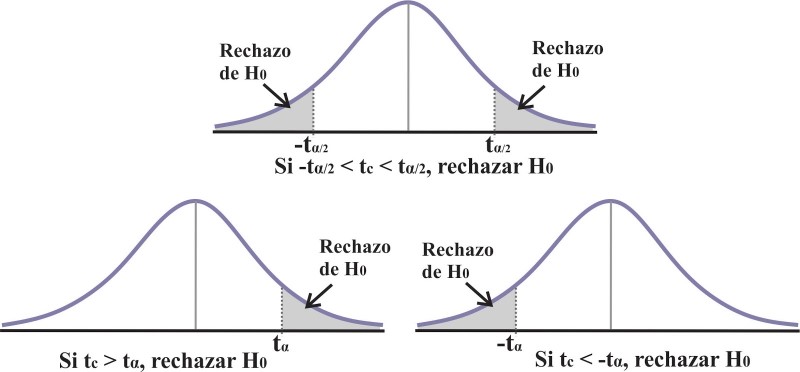
- Determinar el valor p: El valor p es la probabilidad de obtener los resultados observados si la hipótesis nula fuera verdadera.
- Comparar el valor p con el nivel de significancia: El nivel de significancia es un valor que se establece previamente y determina el umbral para rechazar la hipótesis nula. Si el valor p es menor que el nivel de significancia, se rechaza la hipótesis nula.
Ejemplo de aplicación de la prueba t de Student
Imagine que un investigador desea evaluar la eficacia de un nuevo medicamento para tratar la ansiedad. El investigador recluta a 20 participantes y los divide aleatoriamente en dos grupos: un grupo de control que recibe un placebo y un grupo de tratamiento que recibe el nuevo medicamento. Después de un período de tiempo determinado, el investigador mide los niveles de ansiedad de los participantes utilizando un cuestionario estandarizado.
Para determinar si el nuevo medicamento es eficaz, el investigador puede utilizar una prueba t de muestras independientes. La hipótesis nula sería que no hay diferencia en los niveles de ansiedad entre los dos grupos. La hipótesis alternativa sería que sí hay una diferencia en los niveles de ansiedad entre los dos grupos.
El investigador calcularía el estadístico t y el valor p. Si el valor p es menor que el nivel de significancia (por ejemplo, 0.05), el investigador rechazaría la hipótesis nula y concluiría que el nuevo medicamento es eficaz para tratar la ansiedad.
Ventajas y desventajas de la prueba t de Student
La prueba t de Student tiene varias ventajas, incluyendo su simplicidad, su capacidad para manejar datos con tamaño de muestra pequeño y su amplia aplicación en diferentes campos.
Ventajas
- Sencilla de aplicar: La prueba t de Student es relativamente fácil de realizar, incluso con software estadístico.
- Robusta: La prueba t de Student es robusta a las violaciones de la normalidad, especialmente con tamaños de muestra grandes.
- Amplia aplicación: La prueba t de Student se puede utilizar para analizar una variedad de datos, como datos de comportamiento, datos médicos y datos financieros.
Desventajas
- Suposiciones: La prueba t de Student tiene algunas suposiciones que deben cumplirse para que los resultados sean válidos. Estas suposiciones incluyen la normalidad de los datos y la igualdad de varianzas.
- Tamaño de muestra pequeño: La prueba t de Student puede ser menos potente con tamaños de muestra pequeños.
- Sensible a valores atípicos: La prueba t de Student puede ser sensible a valores atípicos, que pueden afectar significativamente los resultados.
Consideraciones importantes al utilizar la prueba t de Student
Al utilizar la prueba t de Student, es importante tener en cuenta las siguientes consideraciones:
- Tamaño de la muestra: La prueba t de Student es más potente con grandes tamaños de muestra.
- Normalidad de los datos: La prueba t de Student asume que los datos se distribuyen normalmente. Si los datos no son normales, se pueden utilizar otras pruebas, como la prueba de Wilcoxon.
- Igualdad de varianzas: La prueba t de Student asume que las varianzas de los grupos son iguales. Si las varianzas no son iguales, se puede utilizar una versión modificada de la prueba t.
- Valores atípicos: Los valores atípicos pueden afectar significativamente los resultados de la prueba t de Student. Se recomienda verificar los datos para detectar valores atípicos y tratarlos de manera adecuada.
La prueba t de Student es una herramienta poderosa para comparar las medias de dos grupos de datos. Esta prueba se utiliza ampliamente en diferentes campos y proporciona una manera sencilla y eficaz de determinar si existe una diferencia significativa entre las medias de los grupos. Al comprender los principios de la prueba t de Student y las consideraciones importantes al utilizarla, los investigadores pueden utilizar esta herramienta de manera efectiva para analizar sus datos y obtener resultados confiables.
¿Qué es la prueba t de Student?
La prueba t de Student es una prueba estadística utilizada para comparar las medias de dos grupos. Se utiliza cuando los datos se distribuyen normalmente y el tamaño de la muestra es pequeño (generalmente menos de 30). La prueba t puede utilizarse para determinar si hay una diferencia significativa entre las medias de los dos grupos o si la diferencia es simplemente debida al azar.
¿Cuáles son los tipos de pruebas t de Student?
Hay dos tipos principales de pruebas t de Student:
- Prueba t de muestra única: se utiliza para comparar la media de una muestra con una media poblacional conocida.
- Prueba t de muestras independientes: se utiliza para comparar las medias de dos grupos independientes.
- Prueba t de muestras pareadas: se utiliza para comparar las medias de dos grupos que están relacionados, como las puntuaciones de los mismos sujetos antes y después de un tratamiento.
¿Cuáles son los supuestos de la prueba t de Student?
La prueba t de Student tiene varios supuestos que deben cumplirse para garantizar la validez de los resultados. Estos supuestos son:
- Los datos deben distribuirse normalmente.
- Las varianzas de los dos grupos deben ser iguales (para la prueba t de muestras independientes).
- Los datos deben ser independientes (para la prueba t de muestras independientes).
¿Cómo se interpreta la prueba t de Student?
Los resultados de la prueba t de Student se resumen en un valor p. El valor p es la probabilidad de obtener los resultados observados si no hay diferencia real entre las medias de los dos grupos. Si el valor p es menor que el nivel de significancia (generalmente 0.05), se rechaza la hipótesis nula y se concluye que hay una diferencia significativa entre las medias de los dos grupos. Si el valor p es mayor que el nivel de significancia, no se rechaza la hipótesis nula y se concluye que no hay una diferencia significativa entre las medias de los dos grupos.
¿Cuáles son algunas de las limitaciones de la prueba t de Student?
La prueba t de Student tiene algunas limitaciones:
- Es sensible a la violación de los supuestos.
- Puede ser poco potente cuando el tamaño de la muestra es pequeño.
- No es apropiada para datos que no se distribuyen normalmente.
¿Cuándo se debe utilizar la prueba t de Student?
La prueba t de Student es una prueba estadística útil para comparar las medias de dos grupos. Se utiliza cuando los datos se distribuyen normalmente y el tamaño de la muestra es pequeño. La prueba t puede utilizarse para determinar si hay una diferencia significativa entre las medias de los dos grupos o si la diferencia es simplemente debida al azar.