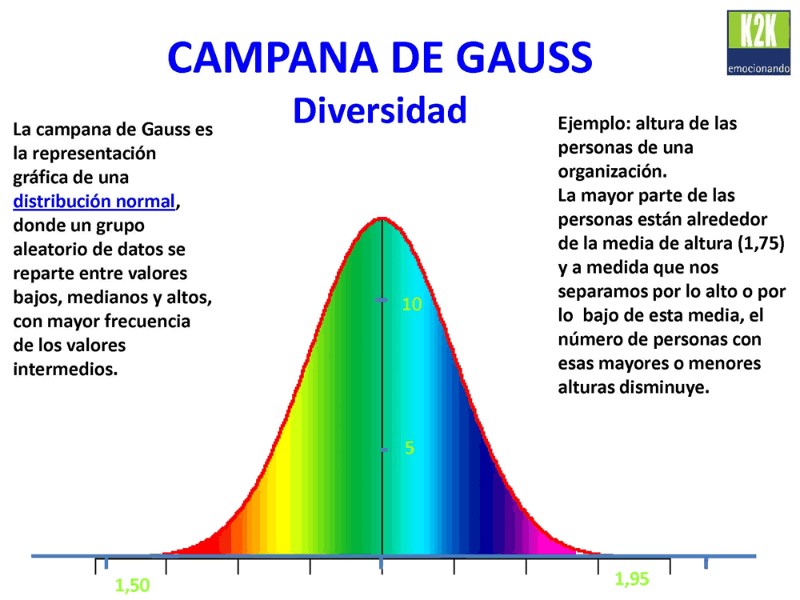
Campana de Gauss: Una herramienta esencial para comprender datos

• La media: Representa el centro de la distribución, la cual coincide con la moda y la mediana en una distribución normal perfecta.
• La desviación estándar: Mide la dispersión de los datos alrededor de la media. Una desviación estándar grande indica una mayor dispersión de los datos, mientras que una desviación estándar pequeña indica una menor dispersión.

Regla 68-95-99.7

Esta regla, también conocida como la regla empírica, establece que:

• 68% de los datos se encuentran dentro de una desviación estándar de la media.
• 95% de los datos se encuentran dentro de dos desviaciones estándar de la media.
• 99.7% de los datos se encuentran dentro de tres desviaciones estándar de la media.

Teorema del límite central

Este teorema establece que, independientemente de la distribución original de los datos, la distribución de la media de las muestras tiende a seguir una campana de Gauss cuando se acumulan suficientes datos. Esto significa que la campana de Gauss se convierte en una herramienta poderosa para el análisis de grandes conjuntos de datos.

Ventajas de la campana de Gauss

La campana de Gauss ofrece varias ventajas que la convierten en una herramienta fundamental para el análisis de datos:

Intuitiva y fácil de entender

Su forma simple la hace accesible para personas sin un profundo conocimiento matemático. La forma de campana es fácil de visualizar y comprender, lo que facilita la interpretación de los datos.

Amplia aplicabilidad

Esta distribución permite modelar una amplia gama de situaciones del mundo real, desde fenómenos naturales hasta comportamientos sociales.

Resumen de información

La media y la desviación estándar resumen la información clave de la distribución, simplificando el análisis. En lugar de tener que analizar todos los datos individualmente, la media y la desviación estándar proporcionan una imagen general de la distribución.

Herramienta poderosa para análisis de datos

El Teorema del límite central convierte la campana de Gauss en una herramienta fundamental para el análisis de grandes conjuntos de datos. Permite realizar inferencias estadísticas y establecer conclusiones significativas sobre la población a partir de una muestra de datos.

Usos de la campana de Gauss

La campana de Gauss tiene aplicaciones en diversas disciplinas, desde la estadística y la física hasta la economía y la psicología.

Estadística descriptiva

Describe la distribución de datos en una población, resumiendo la tendencia central y la dispersión. Permite comprender el comportamiento de los datos y detectar patrones y tendencias.

Inferencia estadística

Permite realizar predicciones y estimaciones, calcular intervalos de confianza y realizar pruebas de hipótesis. Estas herramientas ayudan a tomar decisiones informadas basadas en los datos.

Investigación psicológica

Se utiliza para modelar fenómenos como la distribución de coeficientes de inteligencia (CI), la distribución de rasgos de personalidad o la distribución de puntuaciones en tests psicológicos.

Economía y finanzas

Modela la variabilidad de los rendimientos de activos financieros, como acciones, bonos o divisas. Esto ayuda a los inversores a comprender el riesgo asociado con sus inversiones.

Biología y medicina

Se aplica para analizar datos biométricos, como la altura, el peso o la presión arterial. También se utiliza para evaluar la eficacia de tratamientos médicos y evaluar la distribución de enfermedades.

Control de calidad

Evalúa la consistencia y la variabilidad en la producción de bienes y servicios. Permite identificar posibles problemas de calidad y tomar medidas correctivas.

Modelado de fenómenos naturales

Se utiliza para modelar la distribución de variables como la velocidad del viento, la temperatura o la concentración de sustancias químicas.

Machine learning y ciencia de datos

Se utiliza como suposición inicial en muchos algoritmos y modelos de aprendizaje automático. Permite desarrollar modelos predictivos más precisos y eficientes.

Ejemplos de la campana de Gauss en la vida real

La campana de Gauss se encuentra en muchas áreas de la vida real.

Evaluación de rendimiento académico

En un examen de matemáticas, la campana de Gauss puede ayudar a comprender la distribución de las calificaciones. La media representaría la calificación promedio, y la desviación estándar indicaría la dispersión de las calificaciones alrededor de la media. Con esta información, los educadores pueden identificar áreas de mejora en la enseñanza y establecer estándares de rendimiento.

Distribución de la estatura humana

La estatura humana sigue aproximadamente una distribución normal. La mayoría de las personas tienen una estatura cercana a la media, mientras que un número menor de personas son significativamente más altas o más bajas.

Distribución de la presión arterial

La presión arterial también sigue una distribución normal. La mayoría de las personas tienen una presión arterial dentro de un rango considerado normal, mientras que un número menor de personas tienen presión arterial alta o baja.

Distribución de las puntuaciones en un test de inteligencia

Las puntuaciones en un test de inteligencia (CI) también siguen una distribución normal. La mayoría de las personas tienen un CI dentro de un rango considerado normal, mientras que un número menor de personas tienen un CI muy alto o muy bajo.

La campana de Gauss es una herramienta esencial en análisis estadístico, debido a su simplicidad, versatilidad y capacidad para resumir datos complejos. Su aplicación en diversas disciplinas, desde la física y la biología hasta la economía y la psicología, la convierte en una herramienta fundamental para comprender y modelar fenómenos del mundo real.

La capacidad de la campana de Gauss para modelar la distribución de datos, su aplicación en inferencia estadística y su utilidad para realizar predicciones y estimaciones la convierten en una herramienta esencial para la investigación científica, la toma de decisiones informadas y la comprensión de los fenómenos que nos rodean.

¿Qué es la Campana de Gauss?

La Campana de Gauss, también conocida como distribución normal, es una función matemática que describe la distribución de datos en un conjunto. Se caracteriza por su forma de campana simétrica, con la mayoría de los datos concentrados alrededor de la media y dispersándose uniformemente hacia ambos lados.

¿Cuáles son las características clave de la Campana de Gauss?

Las características principales de la Campana de Gauss incluyen:

• Simétrica: La mitad de los datos se encuentra a la izquierda de la media y la otra mitad a la derecha.
• Media y desviación estándar: La función se define por dos parámetros: la media, que representa el centro de la distribución, y la desviación estándar, que mide la dispersión de los datos.
• 68-95-99.7 regla: Aproximadamente el 68% de los datos se encuentra dentro de una desviación estándar de la media, el 95% dentro de dos desviaciones estándar y el 99.7% dentro de tres desviaciones estándar.
• Teorema del límite central: Independientemente de la distribución original de los datos, cuando se acumulan suficientes datos, la distribución de la media de las muestras tiende a seguir una campana de Gauss.

¿Cuáles son las ventajas de usar la Campana de Gauss?

La Campana de Gauss ofrece varias ventajas:

• Intuitiva y fácil de entender: Su forma simple la hace accesible para personas sin un profundo conocimiento matemático.
• Amplia aplicabilidad: Permite modelar una amplia gama de situaciones del mundo real.
• Resumen de información: La media y la desviación estándar resumen la información clave de la distribución, simplificando el análisis.
• Herramienta poderosa para análisis de datos: El Teorema del límite central la convierte en una herramienta fundamental para el análisis de grandes conjuntos de datos.

¿Para qué se utiliza la Campana de Gauss?

La Campana de Gauss tiene diversas aplicaciones, entre las que se incluyen:

• Estadística descriptiva: Describe la distribución de datos en una población, resumiento la tendencia central y la dispersión.
• Inferencia estadística: Permite realizar predicciones y estimaciones, calcular intervalos de confianza y realizar pruebas de hipótesis.
• Investigación psicológica: Se utiliza para modelar fenómenos como la distribución de coeficientes de inteligencia.
• Economía y finanzas: Modela la variabilidad de los rendimientos de activos financieros.
• Biología y medicina: Se aplica para analizar datos biométricos y evaluar la eficacia de tratamientos.
• Control de calidad: Evalúa la consistencia y la variabilidad en la producción de bienes y servicios.
• Modelado de fenómenos naturales: Modelar la distribución de variables como la velocidad del viento, la temperatura o la concentración de sustancias químicas.
• Machine learning y ciencia de datos: Se utiliza como suposición inicial en muchos algoritmos y modelos.

¿Cómo se puede aplicar la Campana de Gauss en la vida real?

Un ejemplo práctico es la evaluación del rendimiento académico. En un examen de matemáticas, la campana de Gauss puede ayudar a comprender la distribución de las calificaciones. La media representaría la calificación promedio, y la desviación estándar indicaría la dispersión de las calificaciones alrededor de la media. Con esta información, los educadores pueden identificar áreas de mejora en la enseñanza y establecer estándares de rendimiento.

¿Qué podemos sacar sobre la Campana de Gauss?

La campana de Gauss es una herramienta esencial en análisis estadístico, debido a su simplicidad, versatilidad y capacidad para resumir datos complejos. Su aplicación en diversas disciplinas, desde la física y la biología hasta la economía y la psicología, la convierte en una herramienta fundamental para comprender y modelar fenómenos del mundo real.